Sagittarius
Витя "интеграторовед" Подлец сквернослов плагиатор
Векторная волна, поднятая вертом, на вегаляпе, достигла и нашей тихой пиратской бухты. ЯТД, должен быть хотя бы один луч разума среди беспросветного мрака тупости. Рубальский сюда не доберётся, потому маяк будет светить.
Изложение шершавым суконным языком математических формул навевает скуку и вызывает отторжение. Основное преимущество этой потыренной с Хабра статьи - в наглядности.
Пару слов о матчасти
Если мы вспомним школьный курс математики, то для построения графика синуса мы использовали круг. В общем-то так и получается, что вращательное движение можно превратить в синусоиду (как и любое гармоническое колебание). Самое лучшая иллюстрация этого процесса приведена в википедии
Вот они, знаменитые вертовские вектора. Ишь, вертятся.
Вообще, легче изучать фиксированный синус или их смесь, а вот векторов спектроанализатор или ИНИ не рисуют.
Придумка Рубальского заключается в том, чтобы
не видеть глазами искажения на стабильном синусе или ином сигнале,
а мерить длину этих векторов, изменение коей в течение цикла вращения и приводит к искажениям сигнала.
Что, в общем-то, одно и то же, ибо связано математической зависимостью, но намного геморнее без симулятора.
Хабр:
Гармонические колебания
Т.е. фактически график синуса получается из вращения вектора, который описывается формулой:
f(x) = A sin (ωt + φ),
где A — длина вектора (амплитуда колебаний), φ — начальный угол (фаза) вектора в нулевой момент времени, ω — угловая скорость вращения, которая равна:
ω=2 πf, где f — частота в Герцах.
Как мы видим, что зная частоту сигнала, амплитуду и угол, мы можем построить гармонический сигнал.
Магия начинается тогда, когда оказывается, что представление абсолютно любого сигнала можно представить в виде суммы (зачастую бесконечной) различных синусоид. Иначе говоря, в виде ряда Фурье.
Я приведу пример из английской википедии. Для примера возьмём пилообразный сигнал.
Пилообразный сигнал
Его сумма будет представлена следующей формулой:
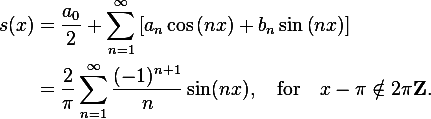
Если мы будем поочерёдно суммировать, брать сначала n=1, затем n=2 и т.д., то увидим, как у нас гармонический синусоидальный сигнал постепенно превращается в пилу:
Наверное красивее всего это иллюстрирует одна программа, найденная мной на просторах сети. Выше уже говорилось, что график синуса является проекцией вращающегося вектора, а как же быть в случае более сложных сигналов? Это, как ни странно, проекция множества вращающихся векторов, а точнее их суммы, и выглядит это всё так:
Вектора рисуют пилу. Вектор - расстояние от центра до границ некой фигуры.
(Представьте, какой гемор ждёт верта при описании сложных колебаний параметрами не ясного всем спектра сигнала, а миллиона векторов, его формирующего. Точнее, формирует-то сигнал источник: инструмент или человек, а теперь предстоит его просчитать и выразить в никому не понятной сумме векторов!
)
Колебания, соотв. ряду Фибоначчи.
bl.ocks.org
Хабр:
Вообще рекомендую сходить самим по ссылке и попробовать самим поиграться с параметрами, и посмотреть как меняется сигнал. ИМХО более наглядной игрушки для понимания я ещё не встречал.
Ещё следует заметить, что есть обратная процедура, позволяющая получить из данного сигнала частоту, амплитуду и начальную фазу (угол), которое называется Преобразование Фурье.
Разложение в ряд Фурье некоторых известных периодических функций (отсюда)
__________________(с)
habr.com
То есть. Верт не придумал ничего умнее, как заменить одно представление синусов на другое.
Ну, и верту говорят:
hydr
Есть несколько способов представления синусоидальных сигналов, в том числе и векторный. Можно в декартовой системе координат но удобней в полярной ( та же рожа только с боку).
В этом случае сигнал представляется вектором заданной амплитуды вращающимся с неизменной угловой скоростью (частотой) и проекция которого на ось абсцисс есть синусоида.
Если у нас имеется периодическая, но несинусоидальная ф-я то для ее векторного представления нам необходимо разложить ее на гармонические ( синусоидальные) составляющие ( это по сути означает снять спектры) каждая из которых будет описываться своим вектором и в этом случае их суммарная проекция на ось абсцисс нарисует нам исходную форму сигнала.
Чисто из интереса, при отсутствии какой либо практической ценности можно попробовать дать векторное описание непериодическому сигналу.
Но тогда нам нужно задать закон вращения вектора во времени ( понятно -скорость вращения будет переменной величиной). Т.е. каким то образом получить аналитическое описания ф-ции и перевести его в поляры. И что? На фига?
Ну хорошо, пусть мы не писатели, мы читатели.
Каким то идеальным способом получили разность двух сигналов у которых несколько отличается форма. Разглядываем (читаем), водим пальцем по вершинам и впадинам этой разности и пытаемся сообразить а где тут вектор?
Во-о-о-т! В этой конкретно взятой, на картинке, точке разность можно описать вектором есть направление и амплитудное значение этой разности. Ура-а-а-а!?
Продвинули палец чуть дальше а тут другой вектор с другими параметрами. А вот эта точка на форме выходного сигнала тютя в тютю совпала с точкой на входном сигнале.
И?
А не будет ни какого И. Будут опять рассказы о том, что все в мироздании есть вектор.
ps
Ежели в чей то голове еще не прояснилось буду задавать один и тот же вопрос - раз искажения векторные дайте оценку этим искажениям в размерности вектора применительно к конкретному у-сю. (с)
То есть, предлагается выразить колебания длины вектора, приводящие к искажениям, в неких единицах, в природе ещё не существующих.
Изложение шершавым суконным языком математических формул навевает скуку и вызывает отторжение. Основное преимущество этой потыренной с Хабра статьи - в наглядности.
Пару слов о матчасти
Если мы вспомним школьный курс математики, то для построения графика синуса мы использовали круг. В общем-то так и получается, что вращательное движение можно превратить в синусоиду (как и любое гармоническое колебание). Самое лучшая иллюстрация этого процесса приведена в википедии
Вот они, знаменитые вертовские вектора. Ишь, вертятся.
Вообще, легче изучать фиксированный синус или их смесь, а вот векторов спектроанализатор или ИНИ не рисуют.
Придумка Рубальского заключается в том, чтобы
не видеть глазами искажения на стабильном синусе или ином сигнале,
а мерить длину этих векторов, изменение коей в течение цикла вращения и приводит к искажениям сигнала.
Что, в общем-то, одно и то же, ибо связано математической зависимостью, но намного геморнее без симулятора.
Хабр:
Гармонические колебания
Т.е. фактически график синуса получается из вращения вектора, который описывается формулой:
f(x) = A sin (ωt + φ),
где A — длина вектора (амплитуда колебаний), φ — начальный угол (фаза) вектора в нулевой момент времени, ω — угловая скорость вращения, которая равна:
ω=2 πf, где f — частота в Герцах.
Как мы видим, что зная частоту сигнала, амплитуду и угол, мы можем построить гармонический сигнал.
Магия начинается тогда, когда оказывается, что представление абсолютно любого сигнала можно представить в виде суммы (зачастую бесконечной) различных синусоид. Иначе говоря, в виде ряда Фурье.
Я приведу пример из английской википедии. Для примера возьмём пилообразный сигнал.
Пилообразный сигнал
Его сумма будет представлена следующей формулой:
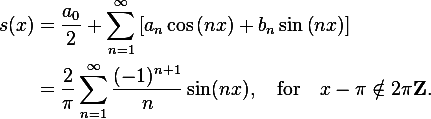
Если мы будем поочерёдно суммировать, брать сначала n=1, затем n=2 и т.д., то увидим, как у нас гармонический синусоидальный сигнал постепенно превращается в пилу:
Наверное красивее всего это иллюстрирует одна программа, найденная мной на просторах сети. Выше уже говорилось, что график синуса является проекцией вращающегося вектора, а как же быть в случае более сложных сигналов? Это, как ни странно, проекция множества вращающихся векторов, а точнее их суммы, и выглядит это всё так:
Вектора рисуют пилу. Вектор - расстояние от центра до границ некой фигуры.
(Представьте, какой гемор ждёт верта при описании сложных колебаний параметрами не ясного всем спектра сигнала, а миллиона векторов, его формирующего. Точнее, формирует-то сигнал источник: инструмент или человек, а теперь предстоит его просчитать и выразить в никому не понятной сумме векторов!
)Колебания, соотв. ряду Фибоначчи.
Fourier series visualisation with d3.js.
Fourier series visualisation with d3.js. GitHub Gist: instantly share code, notes, and snippets.
bl.ocks.org
Хабр:
Вообще рекомендую сходить самим по ссылке и попробовать самим поиграться с параметрами, и посмотреть как меняется сигнал. ИМХО более наглядной игрушки для понимания я ещё не встречал.
Ещё следует заметить, что есть обратная процедура, позволяющая получить из данного сигнала частоту, амплитуду и начальную фазу (угол), которое называется Преобразование Фурье.
Разложение в ряд Фурье некоторых известных периодических функций (отсюда)
__________________(с)
Гармонические колебания
На хабре было несколько статей по преобразованию Фурье и о всяких красивостях типа Цифровой Обработки Сигналов (ЦОС), но неискушённому пользователю совершенно не понятно, зачем всё это нужно и где, а...
habr.com
То есть. Верт не придумал ничего умнее, как заменить одно представление синусов на другое.
Ну, и верту говорят:
hydr
Есть несколько способов представления синусоидальных сигналов, в том числе и векторный. Можно в декартовой системе координат но удобней в полярной ( та же рожа только с боку).
В этом случае сигнал представляется вектором заданной амплитуды вращающимся с неизменной угловой скоростью (частотой) и проекция которого на ось абсцисс есть синусоида.
Если у нас имеется периодическая, но несинусоидальная ф-я то для ее векторного представления нам необходимо разложить ее на гармонические ( синусоидальные) составляющие ( это по сути означает снять спектры) каждая из которых будет описываться своим вектором и в этом случае их суммарная проекция на ось абсцисс нарисует нам исходную форму сигнала.
Чисто из интереса, при отсутствии какой либо практической ценности можно попробовать дать векторное описание непериодическому сигналу.
Но тогда нам нужно задать закон вращения вектора во времени ( понятно -скорость вращения будет переменной величиной). Т.е. каким то образом получить аналитическое описания ф-ции и перевести его в поляры. И что? На фига?
Ну хорошо, пусть мы не писатели, мы читатели.
Во-о-о-т! В этой конкретно взятой, на картинке, точке разность можно описать вектором есть направление и амплитудное значение этой разности. Ура-а-а-а!?
Продвинули палец чуть дальше а тут другой вектор с другими параметрами. А вот эта точка на форме выходного сигнала тютя в тютю совпала с точкой на входном сигнале.
И?
А не будет ни какого И. Будут опять рассказы о том, что все в мироздании есть вектор.
ps
Ежели в чей то голове еще не прояснилось буду задавать один и тот же вопрос - раз искажения векторные дайте оценку этим искажениям в размерности вектора применительно к конкретному у-сю. (с)
То есть, предлагается выразить колебания длины вектора, приводящие к искажениям, в неких единицах, в природе ещё не существующих.
Последнее редактирование:
